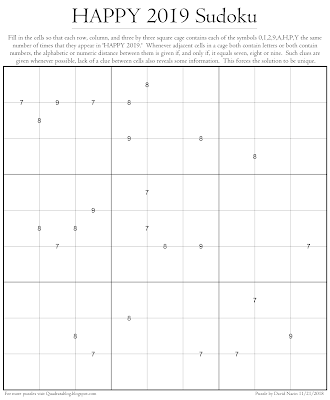
Prime Divisors Latin Square
Today's Latin square puzzle is as tiny as they get, from me at least. (If I made a three by three Latin square puzzle, one could solve it by trying to plug in all twelve possible Latin squares one at a time until they get it right, which for some reason isn't as sporting.)
First, some notation. A prime power is a number that is a power of a single prime number. For example 2, 4, 8, 16, 3, 9, 27, and 81 are all prime powers. The number 6 is not a prime power as you need to use two different primes to write it as a product.
The rules are as follows. A circle indicates that the product of the four numbers in adjacent cells must be a prime power. A shaded circle indicates that the product is a prime power and also that one of the four numbers is divisible by that prime squared.
For example, the numbers 1,2,1,2 would have a product of four which is two squared and thus a prime power. None of those four numbers is individually divisible by two squared, so the circle would not be shaded. The numbers 1,2,4,1 have a product of 8 which is a prime power, and one of the four numbers is divisible by two squared, thus these four numbers would get a shaded circle.
First, some notation. A prime power is a number that is a power of a single prime number. For example 2, 4, 8, 16, 3, 9, 27, and 81 are all prime powers. The number 6 is not a prime power as you need to use two different primes to write it as a product.
The rules are as follows. A circle indicates that the product of the four numbers in adjacent cells must be a prime power. A shaded circle indicates that the product is a prime power and also that one of the four numbers is divisible by that prime squared.
For example, the numbers 1,2,1,2 would have a product of four which is two squared and thus a prime power. None of those four numbers is individually divisible by two squared, so the circle would not be shaded. The numbers 1,2,4,1 have a product of 8 which is a prime power, and one of the four numbers is divisible by two squared, thus these four numbers would get a shaded circle.
It's not a hard puzzle, but I feel there's just enough going on that it still warrants being called a puzzle, which is impressive given its size. It would also fit nice on a business card, if I didn't need a full paragraph for the instructions.


Comments
Post a Comment