Fibsum Associahedron
The upcoming issue of Math Horizons will feature some new puzzles I made, and I decided that I would create four more of that style to post here. As a suggestion from the editor, Tom Edgar, I crated these puzzles over the associahedron graph. We don't need to know anything about the construction of the graph to work on the puzzle.
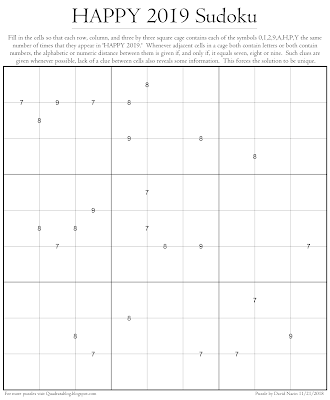
The clues of this puzzle involve the Fibonacci or Pingala-Fibonacci sequence. This is the sequence 0,1,1,2,3,5,8,13,21,... where each number is the sum of the two before it. When the sum of the numbers is adjacent cells is in the sequence, that sum is given. When the sum is not in the sequence, then it is not given. It is important to use the information given by lack of clues in order to solve the puzzle.
The only other rule is that adjacent numbers must have different values. Because of this, all sums have values from 3 to 13. Thus for purposes of this puzzle we only need consider the numbers {3, 5, 8, 13} to be in our set and the numbers {4, 6, 7, 9, 10, 11, 12} to not be in our set.
I use the term Pingala-Fibonacci to refer to the sequence. Pingala's work is the first recording we have of someone discovering the sequence, and he constructed it through the examination of rhythm patterns. I like that idea even better than the famous and entertaining rabbit population exercise that Fibonacci presented in his text over a thousand years later.
Most people would agree that the two puzzles on the top half of the page are easier to solve than the two below, though overall these are probably all on the easier side, once one gets used to the tricks of the rule set. Solutions and a higher quality PDF version can be found at the links below.


Comments
Post a Comment