Parity Adjoku
This week I'm presenting another puzzle variation from my recent book, Math-Infused Sudoku. A pair of numbers is called consecutive if one is exactly one more or one less than the other. Numbers are said to have the same parity if they are either both even or both odd. For example, 4 and 5 are consecutive and of different parity. The numbers 4 and 8 are not consecutive but are of the same parity. The numbers 4 and 7 are neither consecutive nor of the same parity.
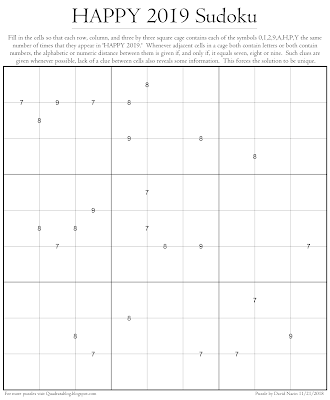
In this puzzle we place a circle between cells whenever they contain consecutive numbers, and a square between cells whenever they are of the same parity. Note that since two numbers can't both be consecutive and have the same parity, there's no chance of both clues appearing between cells. However, since the clues are placed whenever possible, lack of a clue between cells in the same cage indicates that the numbers in those cells are both non-consecutive and also of different parity. Using this last property is necessary in order to arrive at the unique solution.
I'm including two versions of this puzzle: the first is easier and the second is harder. Despite the fact that the harder version has no cells completely revealed at the start, the puzzle only has one solution. In order to ensure this, the center cell must be five or less.
Solution
For a small hint, highlight the white text below:
It is not hard to determine the parity of each cell right at the start, and this is a good way to begin either puzzle.
In this puzzle we place a circle between cells whenever they contain consecutive numbers, and a square between cells whenever they are of the same parity. Note that since two numbers can't both be consecutive and have the same parity, there's no chance of both clues appearing between cells. However, since the clues are placed whenever possible, lack of a clue between cells in the same cage indicates that the numbers in those cells are both non-consecutive and also of different parity. Using this last property is necessary in order to arrive at the unique solution.
I'm including two versions of this puzzle: the first is easier and the second is harder. Despite the fact that the harder version has no cells completely revealed at the start, the puzzle only has one solution. In order to ensure this, the center cell must be five or less.
Solution
For a small hint, highlight the white text below:
It is not hard to determine the parity of each cell right at the start, and this is a good way to begin either puzzle.



Comments
Post a Comment